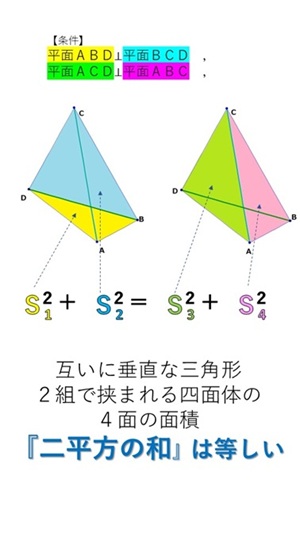
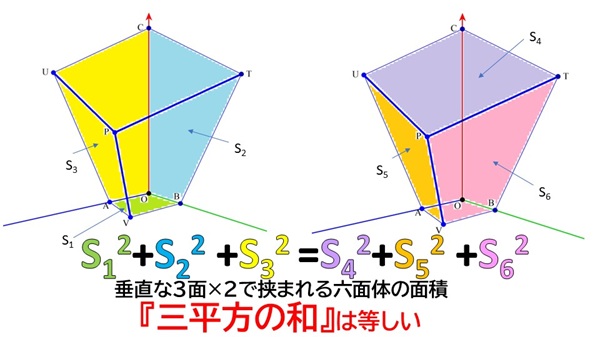
これらの性質が成り立つことの証明です
「Yahoo知恵袋」に投稿したところ、「灰色トム号」さんから、
ものの3時間で、素晴らしい回答をいただきました。
これが、そのURLです。
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13308999768
次のPDFファイルが、私なりにかみ砕いたものです。
メインは「Ⅵ」です。「Ⅲ・Ⅳ」では、ベクトルの外積の知識を用います。
それぞれのPDFファイルからは、ブラウザの「←」(戻る)をクリックして戻ってください。
Ⅰ「長さ法ベクトル」の和は0になる
Ⅱ 任意の多角形において「長さ法ベクトル」の和は0になる
Ⅲ 四面体の「面積法ベクトル」の和は0になる
Ⅳ 四面体の「面積法ベクトル」の和は0になるので・・・
Ⅴ 6つの四角形で囲まれた六面体の「面積法ベクトル」の和は0になる
Ⅵ 等しくなる三平方の和(性質と証明)
Ⅶ 等しくなる三平方の和(具体例で検証)