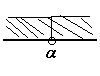
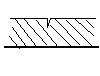
特別な場合（その２）「＞０などを＝０に変えた２次方程式が実数解を持たない場合」

うまい言葉が見つからなくて上のように書きました。
例えば　ｘ２＋ｘ＋１＞０　のような問題です。
　　　　ｘ２＋ｘ＋１＝０　とすると、
　　　　因数分解はできないので解の公式で計算してみると、ルートの中が負になり、
　　　　結局実数解がない…という場合です。

前のページで、くっついてしまった解が、さらに空中に浮いたと考えます。
つまり、実数の解が無いので数直線上に解が取れないということです。
下の図のようになります。この場合イコール付きでも同じ図になります。

　

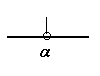
解の図と解の関係

解の図

解

すべての実数

解なし

解説

見たままです。

斜線ないです。

　

例題　ｘ２＋ｘ＋１＞０　を解け。
　　　ｘ２＋ｘ＋１＝０　とすると、
　　　　　−１±√-3
　　　ｘ＝――――――　　となり、ルートの中が負なので、解がない。
　　　　　　　２
　　　従って、ｘ２＋ｘ＋１＞０　の解は、
　　　　の図から、すべての実数である


☆以上で２次不等式裏技は終了です。くれぐれも、ｘ２の係数が負の場合は注意してください。

STEP1へ　STEP2へ　

　　　　　　図が描けそうだが、式が書けそうもない人はこちら

　　　　　　特別な場合（その１）「＞０などを＝０に変えた２次方程式が１つの実数解しかない場合はどうする？」