2jifu04

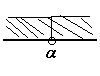
特別な場合（その１）「＞０などを＝０に変えた２次方程式が１つの実数解しかない場合」

うまい言葉が見つからなくて上のように書きました。
例えば　ｘ^２＋６ｘ＋９＞０　のような問題です。
　　　　ｘ^２＋６ｘ＋９＝０　とすると、
　　　　（ｘ＋３）^２＝０　と因数分解され、
　　　　　ｘ＝－３　　　　　　　のように解が１つになってしまう場合です。

この場合は、本当は２つあった解がくっついてしまったと思えばいいだけです。
下の図のようになります。もちろんイコール付きは、●です。

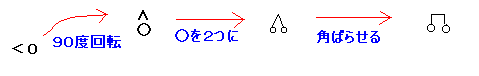
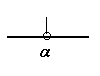
解の図と解の関係

解の図
解	ｘ＝α　を除くすべての実数	すべての実数	解なし	ｘ＝α
解説	ｘ＜α，α＜ｘでも良いが、カッコ悪い。 αは斜線が無い部分なので。	すべての部分に斜線が塗られている。（ｘ＝αの部分も含む）	斜線の引かれているところがない。	αの部分だけ●なので、これだけが解になる。

例　ｘ^２＋６ｘ＋９＞０　の解は　　ｘ＝－３を除くすべての実数
　　ｘ^２＋６ｘ＋９≧０　の解は　　すべての実数
　　ｘ^２＋６ｘ＋９＜０　の解は　　解なし
　　ｘ^２＋６ｘ＋９≦０　の解は　　ｘ＝－３