◆
【探究の経緯】
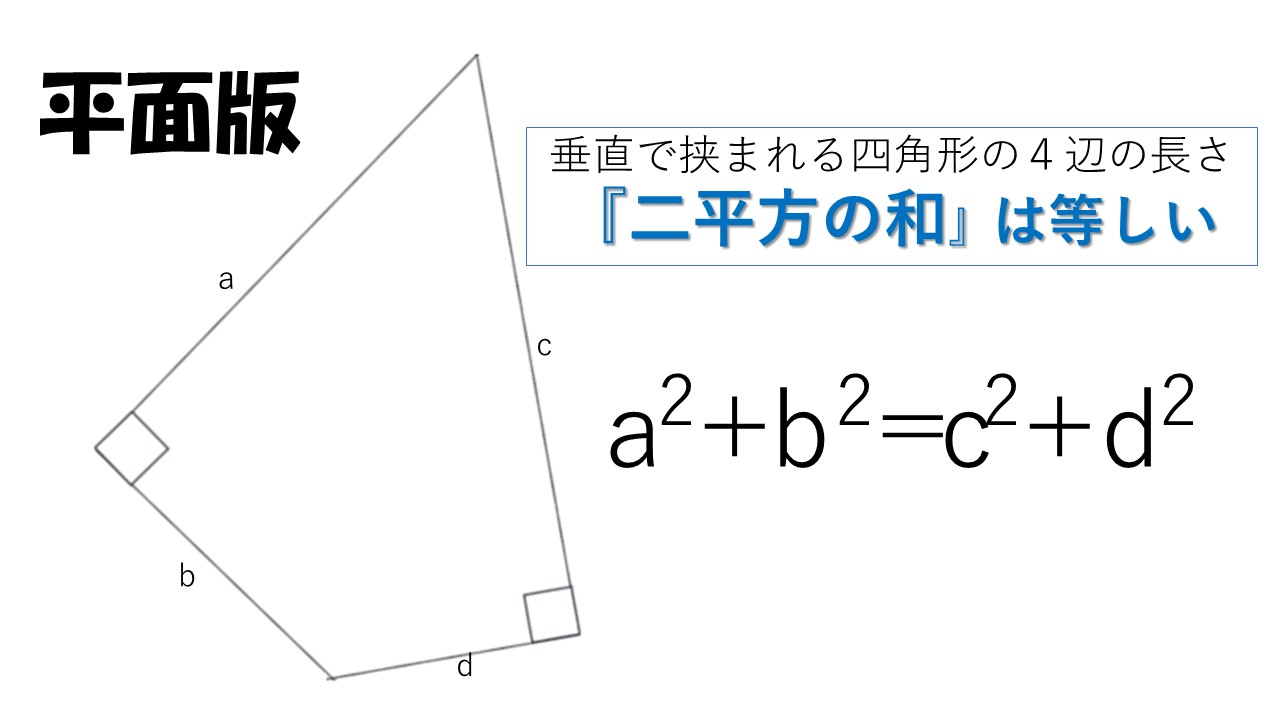
この空間版を検証してみました。
◆
【三平方の和-性質】
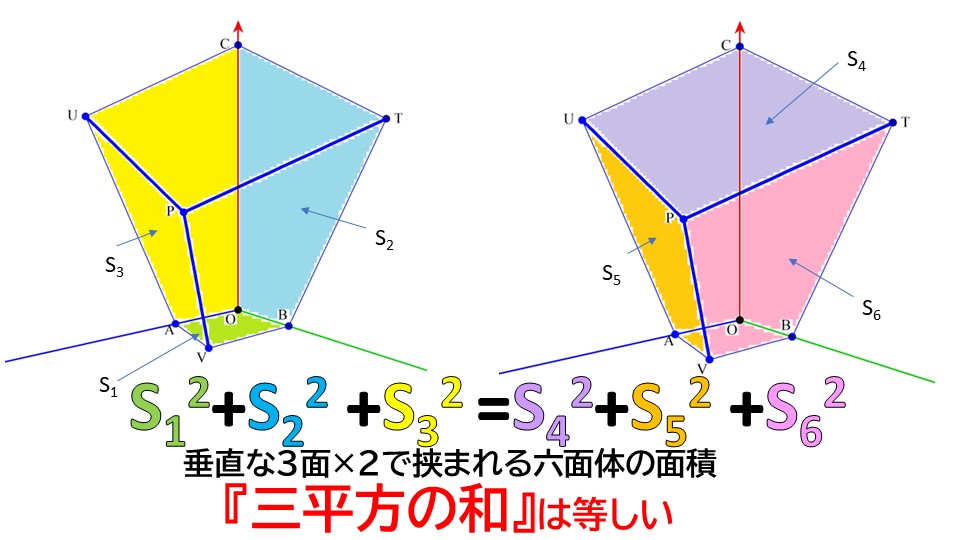
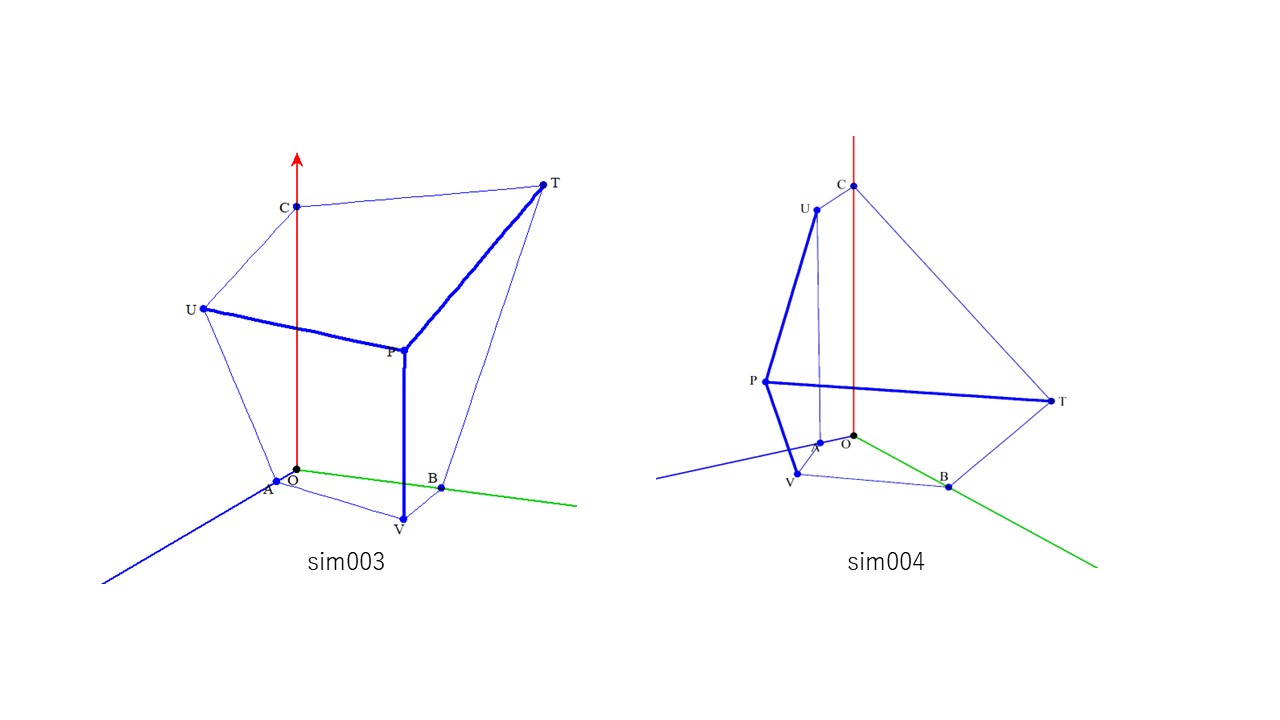
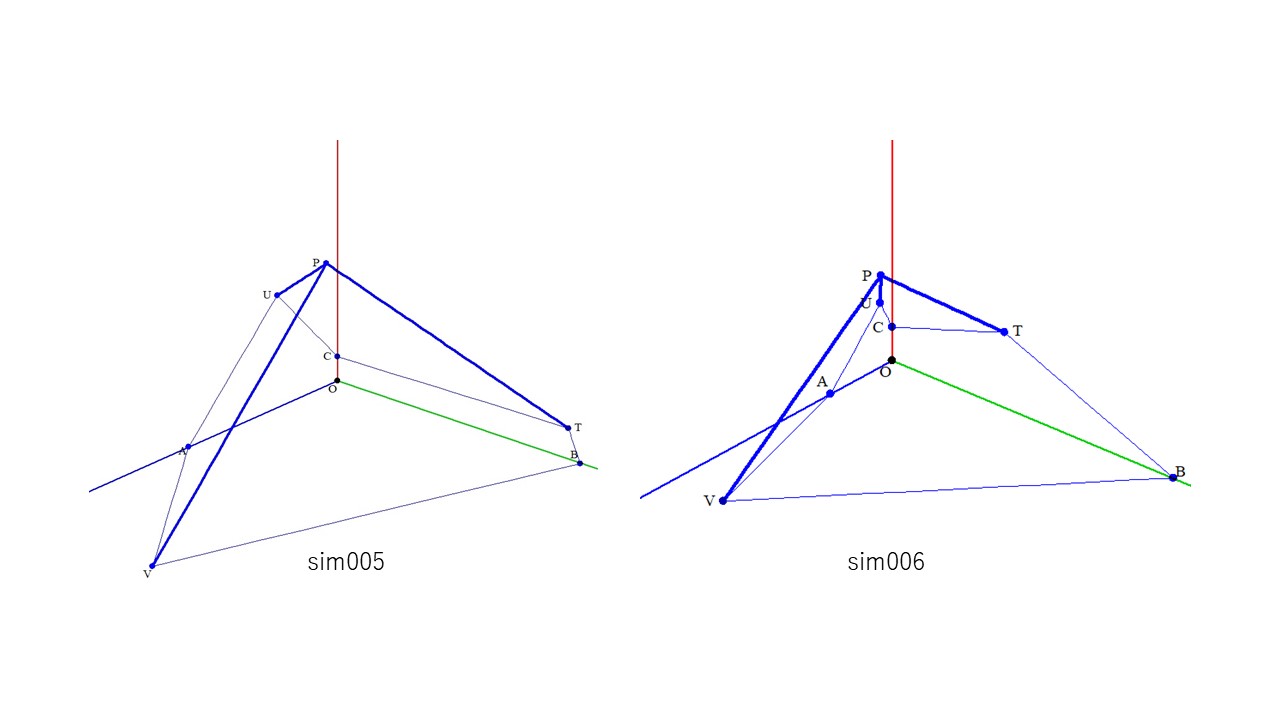
上は、∠AOB=∠BOC=∠COA=∠TPU=∠UPV=∠VPT=90° の六面体。
各面の面積を上のように、S1~S6とおくと、
それぞれの面積の2乗の和について、
S1^2+S2^2+S3^2=S4^2+S5^2+S6^2
が成り立つ
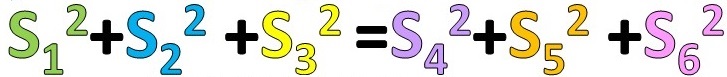
◆
エクセルを使ってシミュレーションしたところ
すべてのシミュレーションにおいてこの等式が成り立ちました。
S1^2+S2^2+S3^2=S4^2+S5^2+S6^2
◆
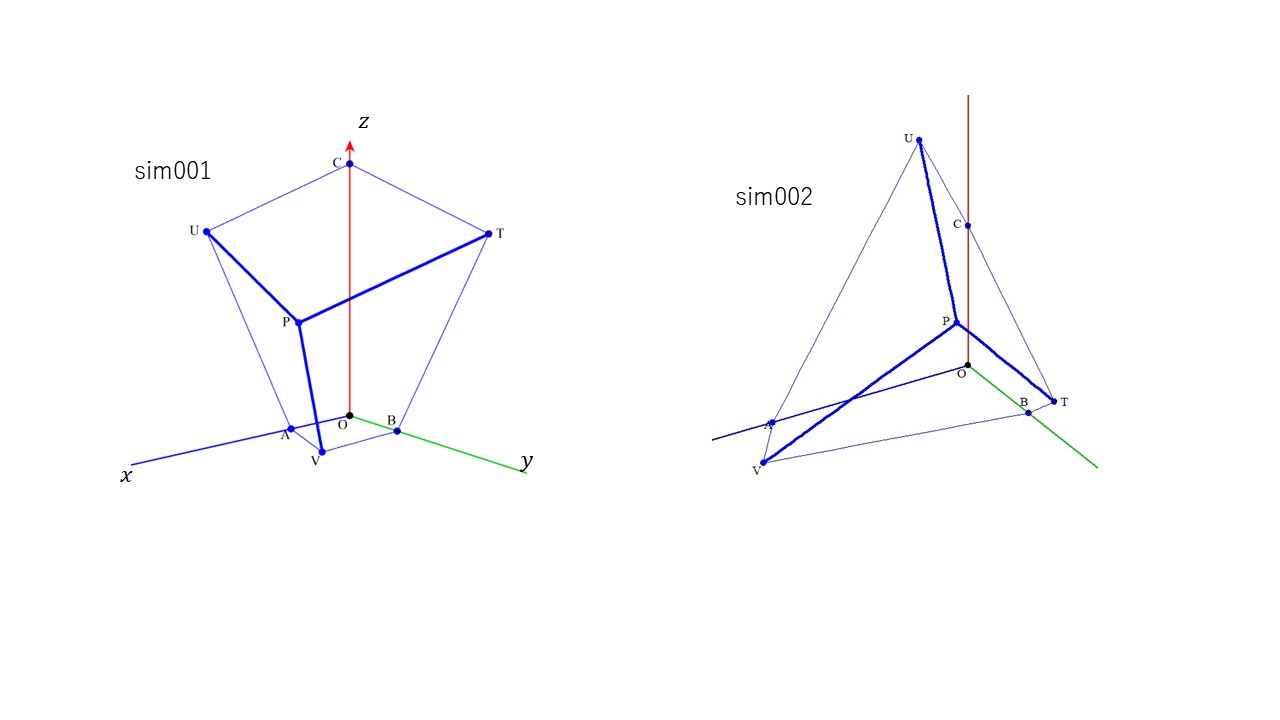
下は六面体の一例です。
◆
◆
2024年9月23日。これが正しいことが示せました!
(足掛け2年に渡る挑戦でした)
ベクトルとエクセルを用いた証明です
00-三平方の和の証明(PDFファイル)
以下は証明に用いたエクセルファイルです。
中を一つ一つ検証しても面白いと思える人はいないと思うので、
誰も中を調べないと思いますが、
証明が間違いではないことを強調する意味で、アップしておきます。
証明に用いたエクセルファイルたち(約86MB)
◆
◆
「雑感」
証明が難しくて、どこを突き進めばいいのかで、大変でした。
・幾何学的な証明
・ベクトルを用いての証明
どちらの証明も試してみました。
幾何学的な証明では、いわゆる「四平方の定理」が使えないものか、
模索しましたが、たどりつけませんでした。
ベクトルを用いた証明では、変数が9個も出てきて、
最初は点Pの座標まで変数にしてみたり、
どこを起点とすればいいのかも試行錯誤でした。
OPの中点を起点とするものも検討しましたが、ダメでした。
証明の前でエクセル計算で、この等式が成り立つことを、
10個くらいの立体でシミュレーションをしていたので、
いつかは、イコールになるはずだということを、
拠り所として、手計算をしてみましたが、
ノートを使って展開するだけでも、
気が遠くなるほどの計算量の上、
一つの計算ミスが命取りになる不安。
四角形の面積計算も、
最初は、二つの三角形に分割してその和で求めましたが、
2本の対角線とそのなす角で四角形の面積が求まることに気づき、路線変更。
それでも計算は気が遠くなり、たびたび挫折。
最終的には、各面の四角形は一つの角が直角であることを利用することにしました。
計算も、意を決して、エクセルにさせました。
途中の計算の過程で、5万項にものぼる項が出てきて、
「これは手計算では、挫折するわけだ」と思いましたね。
エクセルも、途中で理論的なミスに、何度もぶつかり、
試行錯誤の上、最終的に、項が全部消えて、
0になったときは、ガッツポーズが出ていました。
疑問に残ることは、「『面積の2乗』とは何を表すのか?」ということです。
3次元人の私たちは、線分の長さを2乗したものは、
正方形の面積を表すことは理解できます。
かの有名な「三平方の定理」は、正方形の面積の和が等しいことを証明することで、
a^2+b^2=c^3 を示しています。
しかし、いわゆる『四平方の定理』や、
「k1feb15's Mathmatics Idea Box」で紹介している 『二平方の和』や
この『三平方の和』も、どれも、
「面積の2乗」が登場します。
面積の2乗を視覚的に理解できるのは、4次元人からなのでしょうか。
面積の2乗を計算できるのは、数学を習った地球人だけで、
他の惑星に住む知的生物に、これらの定理や性質を説明するのに、
どういう手段を使えばいいのだろうか。
例えば、『三平方の定理』ならば、
正方形3つを書いて、天秤とかで示せるのになぁ。
「面積の2乗」って本当になんなのだろう。
この宇宙のどこでも成り立つ定理や性質なのに。
◆
◆
もしかすると、他のだれかが既に証明しているかもしれませんが、
いろんなWEBサイトを見ても、書籍を見ても、そのようなものは見つかりません。
k1feb15のオリジナルかもしれません。
「三平方の和」という言葉も、勝手に名づけています。
作:k1feb15 2023年8月