「四平方の定理」でも「二平方の定理」でもないよ!

◆
<内容>
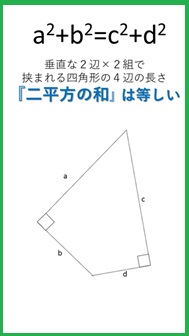
図のように平面上では、互いに垂直な2直線では挟まれる四角形は、
各辺の長さについて、a^2+b^2=c^2=d^2 が成り立ちます。
この3次元版が成り立つのか、検証しました。
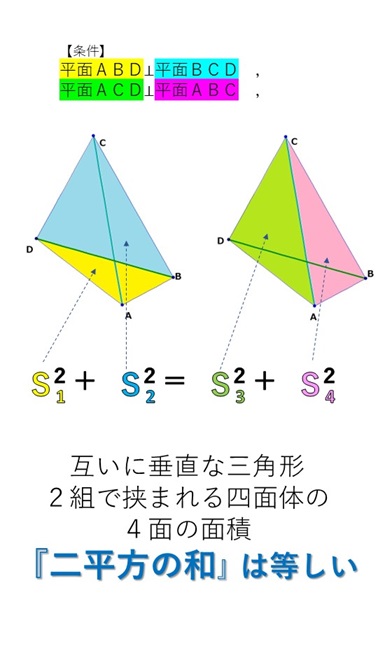
互いに垂直な2平面を2セット組み合わせてできる四面体の
垂直な三角形の面積の組をれぞれS1,S2,およびS3,S4とおくと、
S1^2+S2^2=S3^2+S4^2 が成り立つことが分かりました。
◆
◆
例えばこの立体の座標は、
A(1,1,0),B(0,4/3,0),C(0,0,2),D(0,-1,0)です。
点AからBDに下した垂線をAHとすると、H(0,1,0)で、BD=7/3、AH=1、だから、S1=7/6です。
点CからBDに下した垂線はCOで、 O(0,0,0)で、BD=7/3、CO=2、だから、S2=7/3です。
点DからACに下した垂線をDSとすると、S(1/2,1/2,1)で、AC=√6、DS=(√14)/2、だから、S3=(√21)/2です。
点BからACに下した垂線をBTとすると、T(8/9,8/9,2/9)で、AC=√6、BT=(2√21)/9、だから、S4=(√14)/3です。
ベクトルの内積を計算して0になることから、AH⊥CO、DS⊥BT が成り立っていることが分かります。
S1^2+S2^2=245/36 S3^2+S4^2=245/36 になるので、
S1^2+S2^2=S3^2+S4^2 が成り立っています。
◆
◆
YouTube動画【「二平方の和」は等しい】
◆
◆
証明は、後日紹介します。
「Yahoo!知恵袋」にて、別掲の「三平方の和」の証明を質問したところ、
「灰色トム号」さんの力を借りて、シンプルに証明することができました!!
◆
◆
「二平方の和」という言葉は、勝手に名づけています。
作:k1feb15 2025年1月