STEP3 途中で速さが変化する問題
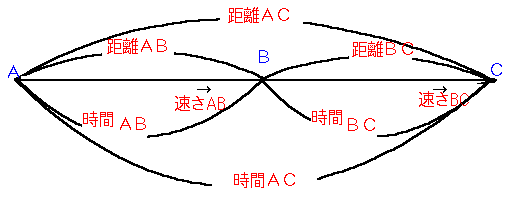
途中で速さが変化する場合は次のような図を描くのが鉄則です。

この中には次の4つの関係式があります。
その4つをすべて使うことを考えれば、答えが求まります。
|
関係ア AB間の 距離 時間・速さ の関係 関係イ BC間の 距離 時間・速さ の関係 関係ウ 距離AB+距離BC=距離AC の関係 関係エ 時間AB+時間BC=時間AC の関係 |
図を描くとき、速さを矢印にしたのは、間違って 速さAB+速さBC=速さAC などと
しないようにです。
例題1
A地点からC地点まで、全部で13kmの道のりを、途中のB地点まで、時速4kmで歩き、解答(中1・方程式を使って)図を実際に描いて、いっしょにやってみてね。
AB間の時間をx時間とする。
分かっている所を記入する。
図を簡略化させてもらいます。
13km
□km □km
A B C
時速4km 時速5km
x時間 □時間
3時間
こんな風になりましたか?
□を埋めていきます。時間BCは関係エより 3−x が入りますね。
道のりABは関係アより 4x が入りますね。
道のりBCは関係イより 5(3-x) が入りますね。
□が埋まったら、まだ使っていない関係ウを使って、方程式を立てます。
4x+5(3-x)=13
これを解いて、x=2 よって答え2時間です。
アドバイス これは時間を求める問題だったので、時間をxとおきましたが、
もしも、道のりを求める問題であっても、時間をxとした方がはるかに楽です。
なぜなら、道のりをxとおくと、分数の方程式が出来てしまうからです。
もちろん、時間をxとして道のりを答える場合は、
答え方を間違えないようにすることはいうまでもありませんが。
例題2
A地点からC地点まで、全部で13kmの道のりを、途中のB地点まで、時速4kmで歩き、解答(中2・連立方程式を使って)実際に書いてみてください。
図を簡略化させてもらいます。
13km
□km □km
A B C
時速4km 時速5km
x時間 y時間
3時間
□を埋める。
関係アより道のりABは4x
関係イより道のりBCは5x
まだ使っていない二つの関係ウ・エを使って連立方程式を立てます。
連立方程式は 4x+5y=13
x+ y=3 です。
これを解いて、x=2 y=1
図中のx,yを2,1 に書き換え、道のりABおよび、道のりBCを求めると、
道のりAB=8km 道のりBC=5km です。